Theory
The PID controller algorithm involves three separate constant parameters called three-term control like the proportional, the integral and derivative values, denoted P, I, and D. Simply, but these values can be interpreted in terms of time: P depends on the present error, I on the accumulation of past errors, and D is a prediction of future errors, based on current rate of change. The weighted sum of these three actions is used to adjust the process via a control element such as the position of a control valve, a damper, or the power supplied to a heating element.
The PID control scheme is named after its three correcting terms, whose sum constitutes the manipulated variable (MV). The proportional, integral, and derivative terms are summed to calculate the output of the PID controller. Defining u(t) as the controller output, the final form of the PID algorithm is:
where
Kp: Proportional gain, a tuning parameter
Ki: Integral gain, a tuning parameter
Kd: Derivative gain, a tuning parameter
e: Error
t: Time or instantaneous time (the present)
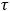
: Variable of integration; takes on values from time 0 to the present t
Proportional term
The proportional term produces an output value that is proportional to the current error value. The proportional response can be adjusted by multiplying the error by a constant Kp, called the proportional gain constant.
The proportional term is given by:
A high proportional gain results in a large change in the output for a given change in the error. If the proportional gain is too high, the system can become unstable. In contrast, a small gain results in a small output response to a large input error, and a less responsive or less sensitive controller. If the proportional gain is too low, the control action may be too small when responding to system disturbances.
Integral term
The contribution from the integral term is proportional to both the magnitude of the error and the duration of the error. The integral in a PID controller is the sum of the instantaneous error over time and gives the accumulated offset that should have been corrected previously. The accumulated error is then multiplied by the integral gain Ki and added to the controller output.
The integral term is given by:
The integral term accelerates the movement of the process towards set point and eliminates the residual steady-state error that occurs with a pure proportional controller. However, since the integral term responds to accumulated errors from the past, it can cause the present value to overshoot the set point value.
Derivative Term
The derivative of the process error is calculated by determining the slope of the error over time and multiplying this rate of change by the derivative gain Kd. The magnitude of the contribution of the derivative term to the overall control action is termed the derivative gain, Kd.
The derivative term is given by:
APPLICATION AND STABILITY OF PID CONTROLLER
EXAMPLE OF PID CONTROLLER :WALL FOLLOWING ROBOT
The robot’s main objective is to follow the wall within a target distance. In order to maintain certain distance from the wall, this is where we applied a digital controller, which is the PID controller. PID controller stands for Proportional, Integral and Derivative Controller which is used to calculate the error between the measured and desired set point and attempts to minimize the error.
The main objective of this robot is to maintain a fixed distance from the side walls. Therefore, PID controller is used to adjust the speed of left and right wheels. The robot for this project is a differential drive robot where the robot movement is controlled by two separately driven motor.
There are three different ways to control the robot movement:
1. Both left wheel and right wheel are moving at the same speed. The robot is in forward linear movement.
2. Both left wheel and right wheel are moving at the same speed, but opposite direction, . The robot will rotate at the midpoint of wheel axis.
3. One wheel is moving while the other wheel is in stationary. The robot will rotate, with centre of rotation at the stationary wheel.
The closed loop system for the wall following robot is shown below. The input to the system is the target distance required for the robot to stay from the obstacle. An ultrasonic sensor is used to provide feedback from the robot position. The measured distance indicates how far the robot is from the obstacle. The error will be computed and processed through a speed of motor.
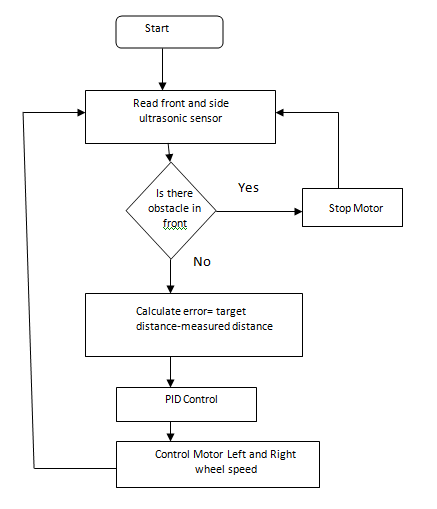
Fig: Flowchart of Wall Following Robot.
The working operation of wall following robot:
Basically the robot will keep on measure the front and side distance from obstacles. If there is any object blocking in front, the robot will stop moving until the obstacles is removed. When no object blocking the robot, Arduino will calculate the error between target distance and measured distance. The error value will pass to PID controller which will be used to control the speed of the left and right wheel.
As seen from the flowchart above, the main priority is first given to the front obstacle. The robot need to ensure that there is no obstacle in front to avoid collision. Only when there is no obstacle, the robot will consider moving in front while keeping the distance from side obstacle.
The method we used to fine tune the PID controller is by trial and error. Based on the understanding on each term, we tried to tune the PID controller to the least oscillation. We start off with pure Proportional (P) controller. It was found out that with pure P controller, the robot would overshoot if the gain is too high. For low gain value, there isn’t any noticeable effect on the robot.
Then we start to introduce the integral (I) and derivative (D) part into the controller. Integral helps the robot to reach the target distance by accumulate the sum of previous errors. Derivative helps the robot to reduce the overshoot compensating the overshoot made from integral part.
Stability
If the PID controller parameters (the gains of the proportional, integral and derivative terms) are chosen incorrectly, the controlled process input can be unstable, i.e., its output diverges, with or without oscillation, and is limited only by saturation or mechanical breakage. Instability is caused by excess gain, particularly in the presence of significant lag.
Generally, stabilization of response is required and the process must not oscillate for any combination of process conditions and set-points, though sometimes marginal stability (bounded oscillation) is acceptable or desired.
Mathematically, the origins of instability can be seen in the Laplace domain. The total loop transfer function is:
where
K(s): PID transfer function
G(s): Plant transfer function
The system is called unstable where the closed loop transfer function diverges for some s. This happens for situations where K(s) G(s)= -1.Typically, this happens when |K(s)G(s)|=1 with a 180 degree phase shift. Stability is guaranteed when K(s) G(s) <1 for frequencies that suffer high phase shifts.
A more general formalism of this effect is known as the Nyquist stability criterion.