Theory
In control theory and stability theory, root locus analysis is a graphical method for examining how the roots of a system change with variation of a certain system parameter, commonly a gain within a feedback system. For example, consider a system like a radio. The radio has a "volume" knob that controls the amount of gain of the system. High volume means more power going to the speakers, low volume means less power to the speakers. As the volume value increases, the poles of the transfer function of the radio change, and they might potentially become unstable. We would like to find out if the radio becomes unstable, and if so, we would like to find out what values of the volume cause it to become unstable. Our current methods would require us to plug in each new value for the volume (gain, "K"), and solve the open-loop transfer function for the roots. This process can be a long one. Luckily, there is a method called the root-locus method that allows us to graph the locations of all the poles of the system for all values of gain, K.
As we change gain, we notice that the system poles and zeros actually move around in the S-plane. This fact can make life particularly difficult, when we need to solve higher-order equations repeatedly, for each new gain value. The solution to this problem is a technique known as Root-Locus graphs. Root-Locus allows you to graph the locations of the poles and zeros for every value of gain, by following several simple rules.
Let's say we have a closed-loop transfer function for a particular system:
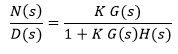
Where N is the numerator polynomial and D is the denominator polynomial of the transfer functions, respectively. Now, we know that to find the poles of the equation, we must set the denominator to 0, and solve the characteristic equation. In other words, the locations of the poles of a specific equation must satisfy the following relationship:
from this same equation, we can manipulate the equation as such:
And finally by converting to polar coordinates:
Now we have 2 equations that govern the locations of the poles of a system for all gain values:
Number of Asymptotes
If the number of explicit zeros of the system is denoted by Z (uppercase z), and the number of poles of the system is given by P, then the number of asymptotes (Na) is given by:
The angles of the asymptotes are given by:
For values of k=0,1,2,…N
a-1
Asymptote Intersection Point
The asymptotes intersect the real axis at the point:
Where ∑P is the sum of all the locations of the poles, and ∑Z is the sum of all the locations of the explicit zeros.
Breakaway Points
The breakaway points are located at the roots of the following equation:
Once you solve for z, the real roots give you the breakaway/re-entry points. Complex roots correspond to a lack of breakaway/re-entry points. The breakaway point equation can be difficult to solve, so many times the actual location is approximated.
Root locus and stability
The root locus procedure should produce a graph of where the poles of the system are for, all values of gain K. When any or all of the roots of D are in the unstable region, the system is unstable. When any of the roots are in the marginally stable region, the system is marginally stable (oscillatory). When all of the roots of D are in the stable region, then the system is stable.
It is important to note that a system that is stable for gain K
1 may become unstable for a different gain K
2. Some systems may have poles that cross over from stable to unstable multiple times, giving multiple gain values for which the system is unstable.
Here is a quick refresher:
Explanation of Table:
This table describes how the concept of stability maps in s-plane and z-plane e.g the region inside the circle of Z-plane and the left hand s-plane are related to each other as it gives a stable region.
In the analysis and design of continuous time control systems, the pole-zero configuration of the transfer function in s-plane is often referred. We know that:
. Left half of s-plane Stable region.
. Right half of s-plane Unstable region.
For relative stability again the left half is divided into regions where the closed loop transfer function poles should preferably be located.
Similarly the poles and zeros of a transfer function in z-domain govern the performance characteristics of a digital system.
Root Locus of Transfer Functions are extremely useful tools for the design of mechanical systems. The root locus can be used to help determine if a system will be stable as well as be used for the design of the natural frequency and damping ratio. Scilab has an easy way to plot the root locus of any transfer function.
Manual
Scilab is a programming language associated with a rich collection of numerical algorithms covering many aspects of scientific computing problems.
Whatever your platform is (i.e. Windows, Linux or Mac), Scilab binaries can be downloaded directly from the Scilab homepage
or from the
Download area.
Scilab elementary mathematical operators:
+ addition
- subtraction
* multiplication
/ right division, i.e. x/y =xy-1
\ left division, i.e. x\y = x-1y
^ power, i.e. xy
** power (same as ^)
' transpose conjugate
In this scilab program
num is the numerator.
den is the denominator.
syslin defines a linear system as a list and checks consistency of data. dom='c' for a continuous time system, dom='d' for a discrete time system, n for a sampled system with sampling period n (in seconds), dom=[] if the time domain is undefined.
clf is used to reset a figure to its default values.
evans is the code to run the root locus plot.
mtlb_axis defines the axis so that asymptotes which appraoch towards infinity, don’t make the important part of the graph too small to read.
Procedure/Program
- Launch scilab 5.3.3 on your computer.
- Write the scilab code given below:
Program
(a)
s=%s;
num=s+2;
den=s*(s+1)*(s^2+3*s+9);
t=syslin('c',num/den);
clf;
evans(t);
mtlb_axis([-5 5 -5 5]);
The graph can be seen below:
Output :
(b)
num=poly([1 0 0 0 0],'s','coeff');
den=poly([0 4 13 1.3 1],'s','coeff');
t=syslin('c',num/den);
clf;evans(t);
mtlb_axis([-5 5 -5 5]);
Here it can be seen that the numerator had a 1 on top and no s terms. On the bottom there was a 0 coefficient for the constant, a coefficient of 4 for the s term, 13 for the s squared term etc. The graph can be seen below:
Output :
Quizzes
Q1.If there are three real poles at -1, -2 and -4, in which directions will the root locus go to infinity? The poles are shown on this plot.
Click on your Answer
(a) +/-60degree, -180degree
(b) 0degree, +/- 120degree
(c) Other
(d)0degree , 120degree,180degree
Answer: a
Q2.In this system there are open-loop poles at s = 0, -2 and -4. Determine where root locus is on the real axis.
Click on any real axis segments where the root
locus is found.
(a) To the left of s = -4
(b) Between s = -4 and s = -2
(c) Between s = -2 and s = 0
(d) To the right of s=0
Answer: b
Q3.In this system there are open-loop poles at s = 0, -2 and -4. Determine the centroid for this system.
The centroid is at s = -2.0
(a) The centroid is at s = -3.0
(b) The centroid is at s = -1.5
(c) The centroid is at s = -2.5
(d) None of the above
Answer: b
Q4. What is the effect of addition of Zeroes on root locus?
(a) To pull the root locus to the left half of s-plane.
(b) To pull the root locus to the right half of s-plane.
(c) To pull the root locus towards origin.
(d) No change
Answer: a
Q5. The roots of the characteristic equation 1+G(s) H(s) are the
(a) Open loop poles of the system
(b) Open loop zeroes of the system
(c) Closed loop poles of the system
(d) Closed loop zeroes of the system
Answer: c